基于 NebulaGraph 的 Betweenness Centrality 算法

​在图论中，介数（Betweenness）反应节点在整个网络中的作用和影响力。而本文主要介绍如何基于 NebulaGraph 图数据库实现 Betweenness Centrality 介数中心性的计算。    

1. 算法介绍

中心性是用来衡量一个节点在整个网络图中所在中心程度的概念，包括度中心性、接近中心性、中介中心性等。 其中度中心性通过节点的度数（即关联的边数）来刻画节点的受欢迎程度，接近中心性是通过计算每个节点到全图其他所有节点的路径和来刻画节点与其他所有节点的关系密切程度。

中介中心性则用于衡量一个顶点出现在其他任意两个顶点对之间最短路径上的次数，从而来刻画节点的重要性。

节点介数中心性的定义是：在所有最短路径中经过该节点的路径数目占最短路径总数的占比。

计算图中节点的介数中心性分为两种情况：有权图上的介数中心性和无权图上的介数中心性。两者的区别在于求最短路径时使用的方法不同，对于无权图采用 BFS（宽度优先遍历）求最短路径，对于有权图采用 Dijkstra 算法求最短路径。

下面所介绍的算法都是针对无向图的。

2. 应用场景

介数反应节点在整个网络中的作用和影响力，主要用于衡量一个顶点在图或网络中承担“桥梁”角色的程度，图中节点 C 就是一个重要的桥梁节点。

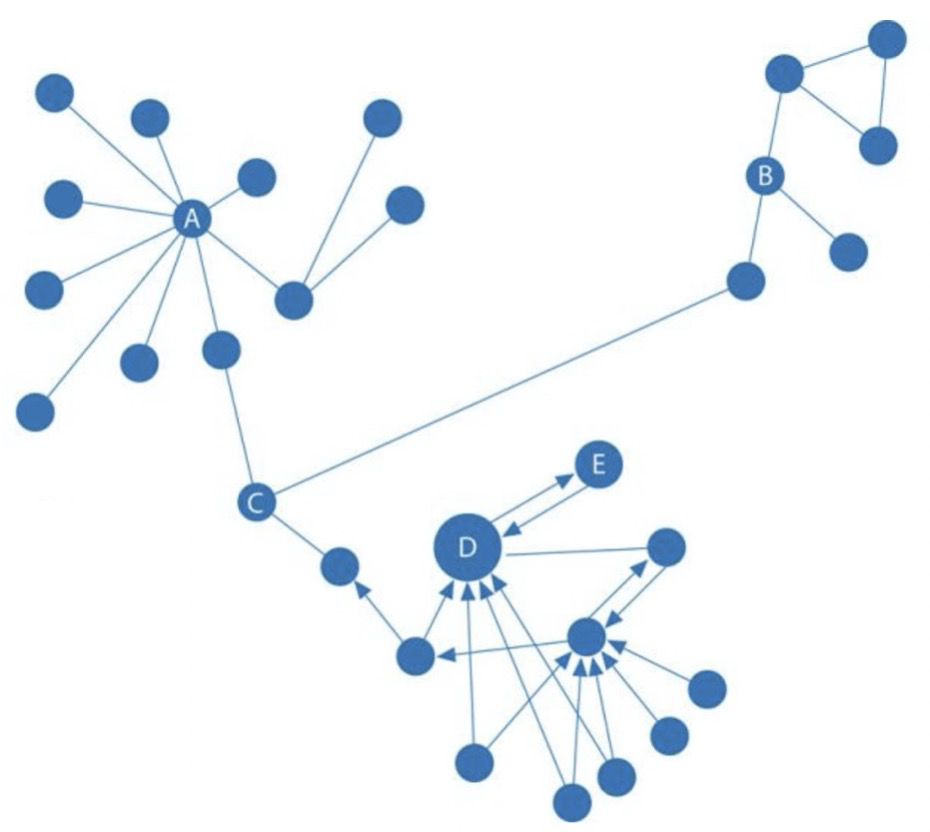
中心性可用于金融风控领域中反欺诈场景里中介实体的识别。也可用于医药领域中特定疾病控制基因的识别，用以改进药品的靶点。

3. 介数中心性公式

节点介数中心性的计算公式如下：

$$C_B = \sum_{s{\not=} v {\not=} t \in V} \frac{\sigma_{st}(v)}{\sigma_{st}}$$

（公式 1）

其中

$$\sigma_{st}(v)$$：经过节点 v 的 s 到 t 的最短路径条数； $$\sigma_{st}$$：节点s到节点t的所有最短路径条数；

s 和 t 是属于节点集合的任意一个节点对。

为方便计算，将每对顶点的介数计算定义为：

$$\delta_{st}(v) = \frac{\sigma_{st}(v)}{\sigma_{st}}$$

（公式 2）

所以上面的公式 1 可以用公式 2 代替，即

$$C_B(v) = \sum_{s{\not=} v {\not=} t \in V} \delta_{st}(v)$$

（公式 3）

4. 求解思路

求节点 v 的介数中心性，即计算 $$\frac{所有(s,t)经过v的最短路径条数}{所有(s,t)之间的最短路径条数}$$，需要知道节点 v 是否在 s 到 t 的路径上。

（1）求节点 v 是否在 s 到 t 的最短路径上，采用下面公式判断($$d_G$$ 表示两点之间的最短路径长度)：

当 v 位于 s 到 t 的最短路径上时，有 $$d_G(s,t) = d_G(s,v) + d_G(v,t)$$

（公式 4）

又因为 $$d_G(s,v)$$ 和 $$d_G(v,t)$$ 是互相独立的，根据数学组合知识得知 s 到 t 的最短路径总数是 s 到 v 的最短路径数与 v 到 t 的最短路径数的乘积。

所以有下面公式：

$$\sigma_{st}(v) = \begin{cases} \sigma_{sv} \times \sigma_{vt} &\text{if } d(s,v) + d(v,t) = d(s,t) \ 0 &\text{if } other
\end{cases}$$

（公式 5）

（2）根据上面公式可得：

节点 s 到节点 t 的经过 w 的最短路径条数为 $$\sigma_{st}(w) = \sigma_{sw} \times \sigma_{wt}$$，在图中节点 v 是 w 的前置节点，所以 st 之间经过节点 v 和 w 的最短路径条数计算公式为：

$$\sigma_{st}(v,{v,w}) = \sigma_{sv} \times \sigma_{wt}$$ 

（公式 6）

下面分为两种情况：分别是 $$t = w$$ 和 $$t \not= w$$

（一）$$t = w$$ 时，不存在$$\sigma_{wt}$$

$$\delta(v,{v,w}) = \frac{\sigma_{sv}}{\sigma_{sw}}$$ 

（公式 7）

（二）$$t \not= w$$ 时

$$\delta(v,{v,w}) = \frac{\sigma_{sw}(v)}{\sigma_{sw}} \times \frac{\sigma_{st}(w)}{\sigma_{st}} $$

（公式 8）

（3）所以将上面两种情况加起来，得到经过 v 的 s 到所有顶点的最短路径数占 s 到所有顶点的最短路径数的比值。

$$\delta_s(v) = \sum_{w:v \in P_s(w)}(\frac{\sigma_{sw}(v)}{\sigma_{sw}} + \sum_{t \not= w \in V}\frac{\sigma_{sw}(v)}{\sigma_{sw}} \times \frac{\sigma_{st}(w)}{\sigma_{st}}) \ = \sum_{w:v \in P_s(w)}\frac{\sigma_{sw}(v)}{\sigma_{sw}}(1 + \sum_{t \not= w \in V} \frac{\sigma_{st}(w)}{\sigma_{st}}) \ = \sum_{w:v \in P_s(w)}\frac{\sigma_{sw}(v)}{\sigma_{sw}} (1 + \delta_s(w)) $$

（公式 9）

其中 $$w:v \in P_s(w)$$即 v 是 s 到 w 路径中 w 的前驱节点。

（4）根据上面的求 $$\delta_{sv}$$ 的公式，下面给出论文中求解无权图时的算法流程，如下所示。

对于无权图实现根据上面流程实现。

有权图的介数中心性计算需要将求解最短路径的方法改成采用 Dijkstra 方法，即改动第一个 while 循环内的代码。

基于 NebulaGraph 的 Betweenness Centrality 实现了针对有权图和无权图的计算，实现代码见 https://github.com/vesoft-inc/nebula-algorithm/blob/master/nebula-algorithm/src/main/scala/com/vesoft/nebula/algorithm/lib/BetweennessCentralityAlgo.scala。

5. 计算示例

首先读取 NebulaGraph 中的图数据，可以指定其边数据进行数据读取。

其次针对 NebulaGraph 的边数据构造拓扑图，执行中心性计算。

读取的 NebulaGraph 图数据以该无权图为例：

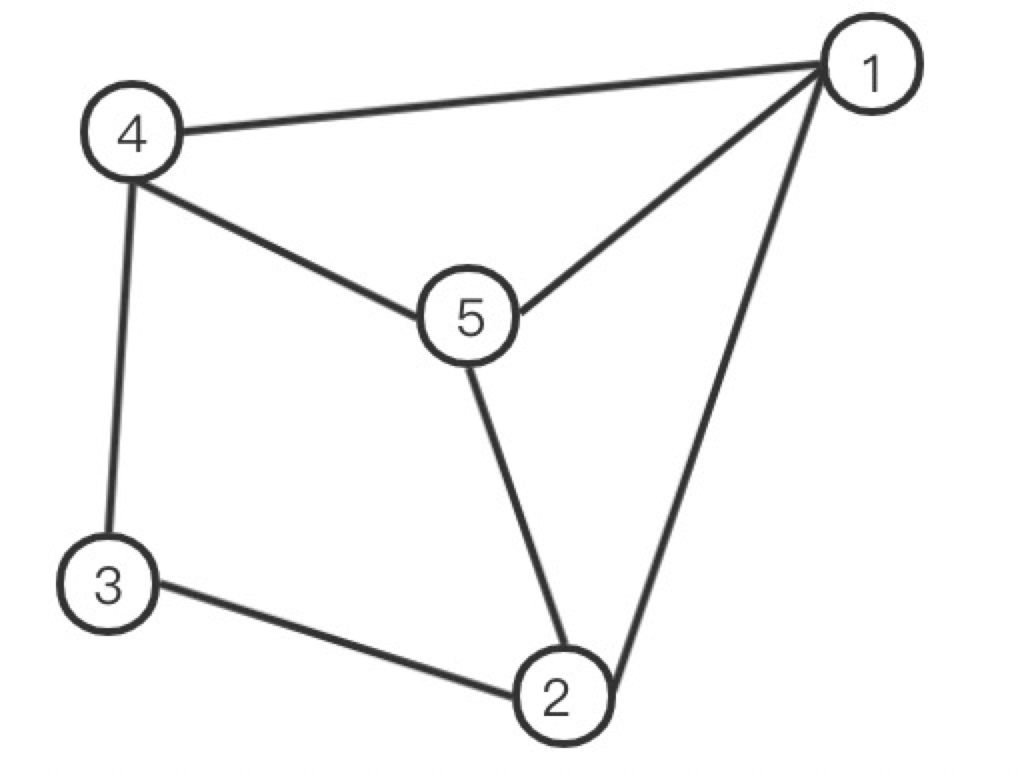
计算节点 1 的 BC：

经过1节点的最短路径节点对	节点对之间的最短路径总数	占通过 1 节点的最短路径数
2-4	3 （2-3-4，2-5-4，2-1-4）	1
节点 1 的 BC：	1/3

计算节点 2 的 BC：

经过 2 节点的最短路径节点对	节点对之间的最短路径总数	占通过 1 节点的最短路径数
1-3	2 （1-2-3，1-4-3）	1
3-5	2（3-2-5，3-4-5）	1
节点 2 的 BC：	1

计算节点 3 的 BC：

经过 3 节点的最短路径节点对	节点对之间的最短路径总数	占通过 1 节点的最短路径数
2-4	3 （2-3-4，2-5-4，2-1-4）	1
节点 3 的 BC：	1/3

计算节点 4 的 BC：

经过 4 节点的最短路径节点对	节点对之间的最短路径总数	占通过 1 节点的最短路径数
1-3	2 （1-4-3，1-2-3）	1
3-5	2（3-4-5.3-2-5）	1
节点 4 的 BC：	1

计算节点 5 的 BC：

经过 5 节点的最短路径节点对	节点对之间的最短路径总数	占通过 1 节点的最短路径数的百分比
2-4	3 （2-3-4，2-5-4，2-1-4）	1
节点 5 的 BC：	1/3

所以每个节点的 BC 值是： 1: 1/3 2: 1 3: 1/3 4: 1 5: 1/3

6. 算法结果示例

数据：读取 NebulaGraph test 中的边数据，以 srcId、dstId 和 rank 分别作为拓扑图中的边的三元组（起点、重点、权重）

(root@nebula) [test]> match (v:node) -[e:relation] -> ()  return e
+------------------------------------+
| e                                  |
+------------------------------------+
| [:relation "3"->"4" @1 {col: "f"}] |
+------------------------------------+
| [:relation "2"->"3" @2 {col: "d"}] |
+------------------------------------+
| [:relation "2"->"5" @4 {col: "e"}] |
+------------------------------------+
| [:relation "4"->"5" @2 {col: "g"}] |
+------------------------------------+
| [:relation "1"->"5" @1 {col: "a"}] |
+------------------------------------+
| [:relation "1"->"2" @3 {col: "b"}] |
+------------------------------------+
| [:relation "1"->"4" @5 {col: "c"}] |
+------------------------------------+

读取 NebulaGraph 边数据，设置无权重并执行 BC 算法，输出结果如下：

vid: 4 BC: 1.0
vid: 1 BC: 0.3333333333333333
vid: 3 BC: 0.3333333333333333
vid: 5 BC: 0.3333333333333333
vid: 2 BC: 1.0

读取 NebulaGraph 边数据，设置有权重并执行 BC 算法，输出结果如下：

vid: 4 BC: 2.0
vid: 1 BC: 0.5
vid: 3 BC: 1.0
vid: 5 BC: 2.0
vid: 2 BC: 0.0

7. 参考资料

• 论文《A Faster Algorithm for Betweenness Centrality》
• Python 的 NetworkX 实现介数中心性的源码：https://github.com/networkx/networkx/blob/master/networkx/algorithms/centrality

本文中如有任何错误或疏漏，欢迎去 GitHub：https://github.com/vesoft-inc/nebula issue 区向我们提 issue 或者前往官方论坛：https://discuss.nebula-graph.com.cn/ 的 建议反馈 分类下提建议 👏；交流图数据库技术？加入 Nebula 交流群请先填写下你的 Nebula 名片，Nebula 小助手会拉你进群~~